Champs scalaires et vectoriels
La représentation de champs scalaires ou vectoriels utilise les bibliothèques numpy et matplotlib.
A partir d'un tableau d'abscisses x et d'un tableau d'ordonnées y, la fonction meshgrid(x, y) renvoie deux tableaux qui constituent un maillage du plan (x,y).
L'instruction X, Y = np.meshgrid(x, y) crée deux tableaux :
- X : valeurs de x pour chaque valeur de y ;
- Y : valeurs de y pour chaque valeur de x.
Champs scalaires - lignes de niveau
On souhaite dans la suite représenter une fonction en tout point M(x,y) d'un domaine sous la forme d'une image en couleurs (dont la couleur évolue en fonction de la valeur de la fonction).
Le code commenté ci-dessous explique la marche à suivre avec un exemple simple : la fonction à représenter, notée Z, vaut la somme des coordonnées : \(Z(x,y) = x+y\).
Dans une représentation en 3 dimensions, Z(x,y) serait un plan (des lignes de niveau iso-Z sont également tracées) :
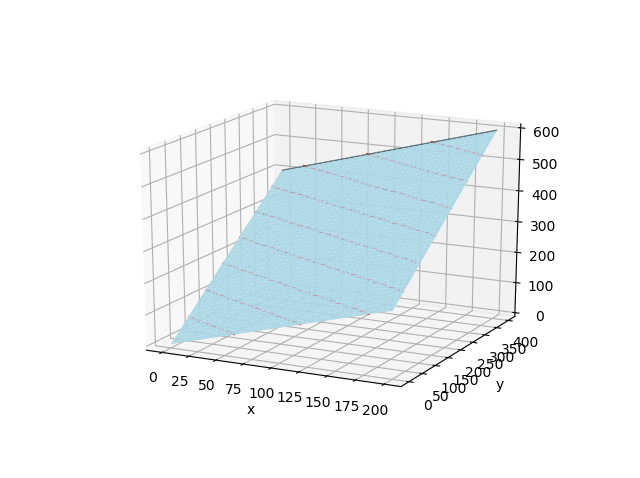
Pour visualiser la valeur de Z dans une représentation en 2 dimensions, on utilise des couleurs et/ou des lignes de niveau.
La fonction contourf (contour + fill = contour et remplissage) permet d'associer des couleurs aux valeurs de Z.
cf = plt.contourf(X, Y, Z, n) colorie le plan en n zones de couleurs uniformes.
plt.colorbar(cf) permet d'afficher une échelle de teintes associée aux valeurs de Z.
meshgrid
Exemple
On utilise dans cet exemple la fonction imshow() pour afficher l'image (cf. pages de ce site consacrées au traitement des images).
Afficher (print) les tableaux X, Y et Z afin de bien comprendre le procédé.
En pratique, il est bien entendu souhaitable d'augmenter la résolution de l'image en augmentant le nombre de points.
meshgrid et contourf
Principe
Autres échelles de teintes
Le paramètre cmap (color map) permet de choisir une échelle de teintes ; par curiosité : échelles de couleurs prédéfinies dans matplotlib.
contourf et contour
L'instruction contour(X, Y, Z, n) permet de tracer n lignes de niveau dans l'image : les lignes telles que la quantité notée Z reste constante et d'afficher les valeurs
correspondantes.
isoLignes = plt.contour(X, Y, Z, 10, colors='k')
plt.clabel(isoLignes) affiche les valeurs associées aux contours tracés.
Variante : valeurs souhaitées pour les contours listées explicitement.
Champs vectoriels - lignes de champ
On souhaite dans la suite représenter un vecteur \(\vec u\) en tout point M(x,y) d'un domaine.
streamplot
Soit le champ \( \vec u \) défini en coordonnées cartésiennes dans le plan par : \(\vec u \left| \begin{array}{l} x+y \\ \displaystyle\frac{x^2}{10}-y \\ \end{array} \right.\)
Il est possible de préciser les points pour lesquels on veut tracer les lignes de champ : cf. start_points.
quiver
Il existe une autre façon de représenter des champs : cf. quiver.