Prisme
Prérequis - Lire la page : Différents aspects de la lumière
Définitions - Vocabulaire
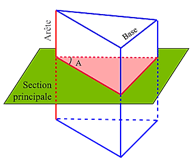
Un prisme est un milieu transparent et homogène d’indice n limité par deux dioptres plans non parallèles qui constituent les faces du prisme ;
celles-ci se coupent suivant une droite qui est l'arête du prisme.
Tout plan perpendiculaire à l'arête est un plan de section principale ; son intersection avec les deux faces définit ce que traditionnellement on appelle l'angle A du prisme.
Généralement un troisième plan limite le milieu réfringent parallèlement à l'arête, c'est la base du prisme.
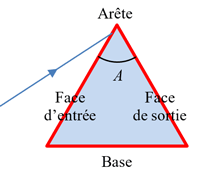
En pratique, on ne prend en considération que les seuls rayons lumineux contenus dans un plan d'incidence normal à l'arête et la représentation du prisme se limite à sa section principale,
c'est à dire à un triangle.
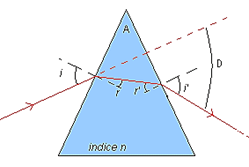
En général le prisme est plongé dans l'air. Dans ces conditions le prisme est totalement défini par son angle A et son indice n.
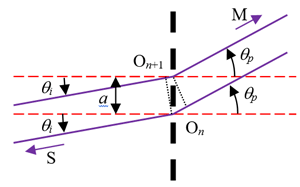
En pratique, le prisme est utilisé en incidence rasante au voisinage de son sommet (au voisinage de l’arête, cf. schéma ci-dessus) mais par souci de clarté les schémas font souvent
figurer des rayons frappant la face d’entrée loin de l’arête (cf. schéma ci-dessous).
Le terme « incidence rasante » signifie que le rayon incident « rase » la face d’entrée ou que l’angle d’incidence i mesuré par rapport à la normale est grand.
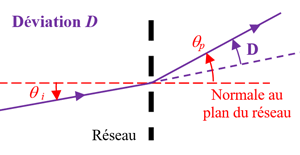
La déviation D est l’angle entre le rayon incident et le rayon émergent (schéma ci-dessus).
Actions d'un prisme sur la lumière
Déviation
A l’aide d’un laser et d’un prisme, visualiser la déviation de la lumière par le prisme et l’existence de rayons réfléchis.
En faisant varier l’angle d’incidence i, visualiser l’existence de réflexion(s) totale(s) à l’intérieur du prisme. Faire des photographies ou des schémas.
Dispersion
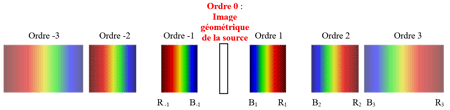
Prisme éclairé en lumière blanche :
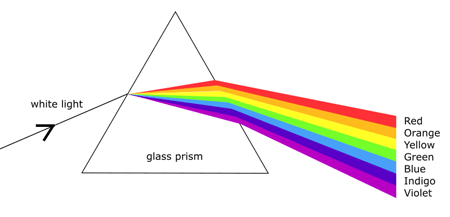
Dispersion par un prisme
Comment interprète-t-on le phénomène de dispersion ?
Peut-on justifier simplement que le bleu est plus dévié que le rouge ? Faire un schéma en couleur.
L’étude qualitative de la déviation (nécessaire en spectroscopie) est présentée dans la suite.
L’étude mathématique détaillée du prisme et de la déviation sont hors programme, à titre indicatif ce
lien concerne cette étude.
Minimum de déviation
Lorsque l’angle d’incidence i varie la déviation D, qui dépend de i d'après les observations précédentes, passe par une valeur minimum \(D_m\) pour une certaine valeur \(i_0\) de l’angle d’incidence.
Le repérage de ce minimum de déviation \(D_m\) joue un rôle essentiel dans les protocoles de mesure en spectroscopie.
Applet
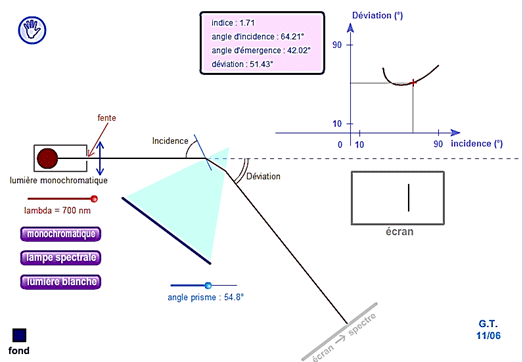
Pour visualiser ce phénomène, on commence par le simuler à l’aide d’une applet :
choisir une lumière monochromatique et faire pivoter le prisme à la souris tout en observant la déviation et le point correspondant sur la courbe \(D(i)\) en haut à droite de la fenêtre de l’applet
(copie d’écran ci-dessous).
Expérimenter en faisant varier divers paramètres (longueur d'onde, angle du prisme, nature de la source).
Observer en particulier que la déviation passe par un minimum. Pour cela, visualiser :
- la courbe \(D(i)\)
- l'angle de déviation (entre rayon incident et émergent)
- l'aspect de l'écran (on voit la raie effectuer un demi-tour au voisinage du minimum de déviation).
On cherche ensuite à repérer expérimentalement le minimum de déviation avec le prisme posé sur un support élévateur et un laser, en obervant sur un écran :
- se placer en incidence rasante au voisinage de l'arête (parfois la base du prisme est noircie ou en verre dépoli sinon la base est quelconque) ;
- en faisant pivoter le prisme toujours dans le même sens autour de son arête, observer que l'image sur l'écran effectue un demi-tour ;
- revenir à la position initiale en faisant pivoter le prisme en sens inverse ; le même phénomène est observé.
Le minimum de déviation est obtenu à la position exacte du prisme correspondant au demi-tour.
Le repérage de la position exacte du prisme correspondant au demi-tour, c'est à dire au minimum de déviation \(D_m\), sera effectué à l'aide d'un goniomètre et cette mesure de \(D_m\) sera exploitée en spectroscopie (par exemple pour déterminer une longueur d'onde).