Historique

D’après https://fr.wikipedia.org/wiki/Optique

L'optique apparaît dès l'Antiquité puis est développée par les érudits musulmans dont des Perses. Elle est d'abord géométrique. Ibn al-Haytham (965-1039), scientifique perse, connu par les occidentaux sous le nom d'Alhazen est considéré comme le père de l'optique moderne, de la physique expérimentale et de la méthode scientifique. Une traduction latine d'une partie de ses travaux, le Traité d'optique, a exercé une grande influence sur la science occidentale.

L'optique géométrique propose une analyse de la formation des images basée sur des principes simples, en termes de rayons lumineux.
L'optique physique ou optique ondulatoire considère la lumière comme une onde ; elle permet d’interpréter les phénomènes d'interférence, de diffraction et de polarisation.
Au début du XXe siècle les théories d'Einstein sur la nature corpusculaire de la lumière donneront naissance au photon et à l'optique quantique.
Les physiciens sont alors contraints d'admettre que la lumière présente à la fois les propriétés d'une onde et d'un corpuscule. Autrement dit, en fonction des expériences, la lumière manifeste soit un comportement ondulatoire soit un comportement corpusculaire.
À partir de là, Louis de Broglie considère, au travers de la mécanique ondulatoire, que si le photon peut se comporter comme un corpuscule, alors, à l'inverse, les corpuscules tels que les électrons ou les protons peuvent se comporter comme des ondes (Cf. rubrique physique moderne sur ce site).


Domaines de l’optique

D’après https://fr.wikipedia.org/wiki/Optique

Optique géométrique (Alhazen)

Caustique

Source : Physique et simulations numériques (J-J Rousseau)

L'optique géométrique s'est développée sur la base d'observations simples et repose sur deux principes et des lois empiriques :

  • la propagation rectiligne dans un milieu homogène et isotrope ;
  • le principe du retour inverse qui exprime la réciprocité du trajet lumineux entre source et destination ;
  • les lois de Snell-Descartes pour la réflexion et la réfraction.

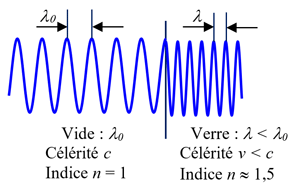
L'optique géométrique, qui est une théorie purement phénoménologique et ne fait pas d'hypothèse sur la nature de la lumière, se trouve validée a posteriori par l'optique ondulatoire, en faisant l'approximation que tous les éléments utilisés sont de grande dimension devant la longueur d'onde de la lumière.


Optique ondulatoire ou optique physique (Huygens-Fresnel, Young, Maxwell)

Diffraction rectangle Michelson coin d'air Plastic Protractor Polarized 05375

Le modèle de l'onde scalaire permet d'interpréter les phénomènes de diffraction (lors du passage par un trou, une fente étroite, près d'un bord...) et d'interférences.
Il faut ensuite considérer qu'il s'agit d'une onde transversale, si on veut interpréter les phénomènes de polarisation.
Enfin, Maxwell permettra de comprendre que les ondes lumineuses ne sont que des ondes électromagnétiques caractérisées par un domaine de longueurs d'ondes qui les rend visibles pour l'homme.

A suivre... (cours d'électromagnétisme et TP d'optique)


Optique quantique

Les problèmes liés au rayonnement du corps noir et à l'effet photoélectrique ont amené à considérer que la lumière était composée de paquets d'énergie (quanta, en allemand, d'après Einstein). Ces phénomènes et d’autres ont conduit à considérer la lumière comme constituée de particules à part entière : les photons.

Les photons sont caractérisés par :

- une masse nulle ;
- une vitesse égale à c (célérité de la lumière) ;
- une énergie \(E = h \nu\) où \(\nu\) est la fréquence de l'onde électromagnétique associée ;
- une quantité de mouvement   \(\vec p = \hbar \vec k\)
Avec   \(\hbar = h / 2 \pi \)   où h désigne la constante de Planck
Et   \(\vec k = \displaystyle\frac{2\pi}{\lambda} \vec u\)  le vecteur d'onde   (\(\vec u\) vecteur unitaire de la direction de propagation).

A suivre... (cours de physique quantique)

La lumière, onde électromagnétique


Onde lumineuse

L’onde lumineuse est caractérisée par :

- sa direction de propagation ;
- sa polarisation ;
- sa fréquence qui ne dépend que du référentiel d’étude (cf. effet Doppler en TP) donc indépendante du milieu.

La longueur d'onde dans le vide, souvent notée \(\lambda_0\), est directement liée à la fréquence ou la période de l'onde : $$ \lambda_0 = \displaystyle\frac{c}{N} = c T $$

La lumière est une onde électromagnétique se propageant à la célérité c = 299 792 458 ms-1 dans le vide (cette valeur fixée par convention définit le mètre à partir de la seconde).


Domaine visible
\(\lambda_0\) en nm380-450450-490490-570570-585585-620620-670
CouleurVioletBleuVertJauneOrangeRouge

Ordres de grandeur pour le domaine visible (connaître) :
fréquence N ≈ 1014 Hz (100 THz), période T ≈ 10-14 s (10 fs).


Milieu de propagation - Indice et longueur d'onde

La longueur d’onde dépend du milieu de propagation via l’indice n caractéristique d’un milieu homogène et isotrope à une fréquence donnée.
L’indice d’un milieu linéaire, homogène et isotrope est :

\(n=\displaystyle\frac{c}{v} \geq 1\)   (onde de célérité c dans le vide et \(v\) dans le milieu considéré).

Rq : l’indice d’un gaz dépend de sa masse volumique (cf. loi de Gladstone).

Indices : nvide = 1 ;nair ≈ 1,0003 ; neau ≈ 1,3 ; nverre ≈ 1,5 (crown) à 1,9 (flint) ; ndiamant ≈ 2,4

Loi de Cauchy
L’indice est fonction de la fréquence N ou de la longueur d’onde dans le vide \(\lambda_0\) : \(n(\lambda _0) = A + \displaystyle\frac{B}{\lambda _0^2}\).

La loi de Cauchy est responsable de la dispersion de la lumière blanche par un milieu via la loi de la réfraction qui fait intervenir l’indice du milieu (cf. prisme).

Longueur d'onde

Onde dans le vide : célérité c et longueur d'onde \(\lambda_0\)
Onde dans un mileu d'indice n : célérité \(v\) et longueur d'onde \(\lambda\)

$$ \left. \begin{align*} &\lambda = v T \\ &\lambda_0 = c T \end{align*} \right\} \Rightarrow \displaystyle\frac{\lambda}{\lambda _0} = \frac{v}{c} = \frac{1}{n(\lambda _0)} $$

D'où :

$$\lambda_{\textrm{milieu}} = \displaystyle\frac{\lambda _0}{n(\lambda _0)} < \lambda _0$$

Longueur d'onde