Barre cylindrique
(d'après CCINP)On considère une barre cylindrique d’axe Ox, de longueur L, de rayon a, de coefficient de conductivité thermique \(\lambda\), comprise entre deux thermostats de
température \(T_1\) et \(T_2\) respectivement en \(x = 0\) et \(x = L\).
L’air extérieur est à la température \(T_0\) et il existe un flux conducto-convectif de coefficient de transfert thermique h entre l’air extérieur et la surface latérale de
la barre.
On se place en régime permanent et \(T_1\) > \(T_2\) > \(T_0\)
- En effectuant un bilan thermique sur une tranche du cylindre de longueur \(dx\), compris entre les abscisses \(x\) et \(x + dx\), déterminer le transfert thermique échangé avec l’air extérieur, que l’on notera \(\delta Q_{ext}\).
- Déterminer l’équation différentielle vérifiée par la température T de la barre.
- Déterminer \(T(x)\).
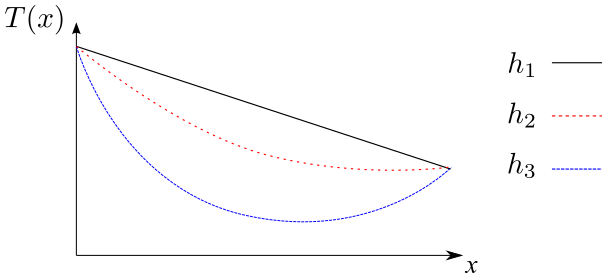
- On donne ci-dessous les courbes représentatives de la température en fonction de la variable x et correspondant à trois valeurs distinctes du coefficient h.
Interpréter ces trois courbes. Déterminer la valeur de \(h_1\) et ranger \(h_i\) par ordre croissant. - On donne le schéma équivalent de la barre cylindrique, déterminer \(R_{cond}\) et \(G_{fuite}\).
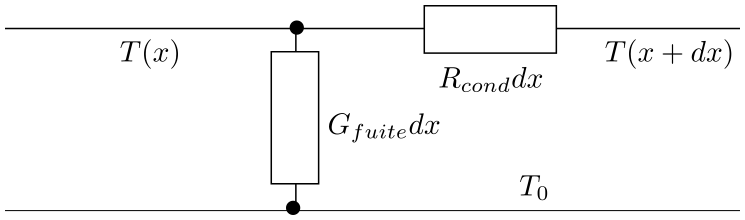
Prérequis :
- Expression du flux convecto-diffusif (loi de Newton).
- Résistance thermique et conditions de validité.
Savoir-faire :
- Réaliser un bilan énergétique sur un système mésoscopique.
- Analogie thermo-électrique.
- \(\delta Q_{ext}\)
- Equation différentielle
- \(T(x)\)
- Courbes
- Schéma équivalent