Système à 3 compartiments


Un récipient à parois rigides et calorifugées est divisé en trois compartiments étanches par deux cloisons mobiles (P1) et (P2) pouvant se déplacer sans frottement.
La cloison (P1) est diathermane tandis que la cloison (P2) est adiabatique (cf. figure ci-dessous).

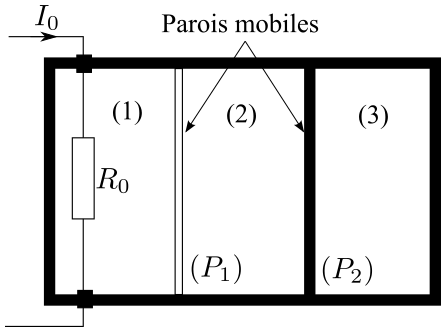
Schéma

Les compartiments (1), (2) et (3) contiennent chacun une mole d’un gaz parfait diatomique.
Un générateur électrique fournit de l’énergie au gaz par l’intermédiaire d’un résistor de résistance \(R_0\), de capacité thermique négligeable, parcouru par un courant constant \(I_0\) pendant une durée \(\tau\). Dans l’état initial, les gaz sont à la même température \(T_0\) et à la même pression \(P_0\). Ils occupent alors chacun le même volume \(V_0\).
On désigne par R la constante des gaz parfaits et par \(\gamma = c_p/c_v\) le rapport des capacités thermiques massiques à pression constante \(c_p\) et à volume constant \(c_v\).
On fait passer un courant suffisamment faible pour que le système évolue lentement. On arrête le chauffage lorsque la température du compartiment (3) vaut : \(T_{3f} = aT_0\) avec \(a > 1\).

  1. Quelle est la pression finale \(P_f\) dans le compartiment 1 ? Dans les autres compartiments ?

  2. Déterminer \(V_{3f}\) final dans (3).

  3. Déterminer \(V_{1f}\) final dans (1)

  4. Déterminer le travail électrique \(W_e\) fourni.

  5. Déterminer la variation d'entropie \(\Delta S\) du système puis l’entropie créée.

    6. On rappelle que l’entropie d’un gaz parfait peut s’écrire :
    \(S(T,V) = nR\left( \dfrac{1}{\gamma-1}\ln\dfrac{T}{T_0} + \ln\dfrac{V}{V_0} \right)\)

Prérequis :

  • Equilibre = équilibre thermique et équilibre mécanique.
  • Puissance, énergie/travail électrique.

Savoir-faire :

  • Evolution isentropique d'un gaz parfait de coefficient \(\gamma\) constant : penser aux lois de Laplace.
  1. \(P_{1f}\)


  2. \(V_{3f}\)


  3. \(V_{1f}\)


  4. \(W_e\)


  5. \(\Delta S\) et \(S_c\)