Mesure de l’écart angulaire de deux étoiles
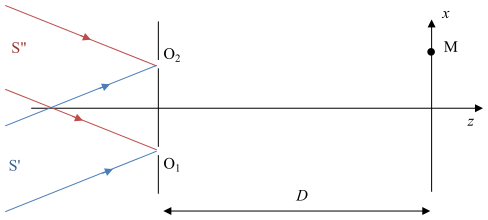
(d'après CCINP)On place deux trous d’Young \(O_1\) et \(O_2\) distants de a le long de l’axe
(Ox) d’un plan de front xOy et on observe l’intensité lumineuse dans le plan transversal \(z = D\) avec \(D >> a\).
Le dispositif est éclairé par une étoile double assimilée à deux sources ponctuelles distinctes \(S'\) et \(S''\) situées à l’infini dans
les directions du plan xOz faisant avec Oz les angles \(\pm\alpha/2\) (voir figure).
On suppose que chacune des étoiles engendre une intensité \(I_0\) sur l’écran quand on bouche un des trous de Young.
On place devant les trous un filtre centré sur la longueur d’onde \(\lambda = 0, 5 \si{μm}\)
- Quelle est l’intensité sur l’écran quand on bouche un des trous ?
- On éteint S".
- Déterminer l’expression de la différence de marche \(\delta^{\prime}\) en un point M de l’écran, pour les ondes provenant de S'.
- Donner l’expression de l’intensité sur l’écran en fonction de \(\delta^{\prime}\).
- Calculer l’interfrange \(\Delta\) pour a = 1 mm, et D = 2 m.
- Exprimer l’intensité sur l’écran en présence des deux étoiles S' et S".
On augmente a en partant d’une valeur faible. Calculer la plus petite valeur \(a_m\) permettant de brouiller les franges pour \(\alpha = 10^{−6} \si{rad}\) et D = 2 m.
Dans la suite, aucun trou n’est bouché.
Prérequis :
- Source cohérente vs incohérente
- Expressions de la différence de marche et de l'interfrange pour un interféromètre d'Young.
- Formule de Fresnel
Savoir-faire :
- Identification/caractérisation d'une différence de marche à l'aide du théorème de Malus-Dupin.
- Condition de brouillage.
- Intensité
- Une seule étoile, S" éteinte
- Différence de marche \(\delta^{\prime}\)
- Intensité
- Interfrange
- Deux étoiles