Ressort poussé
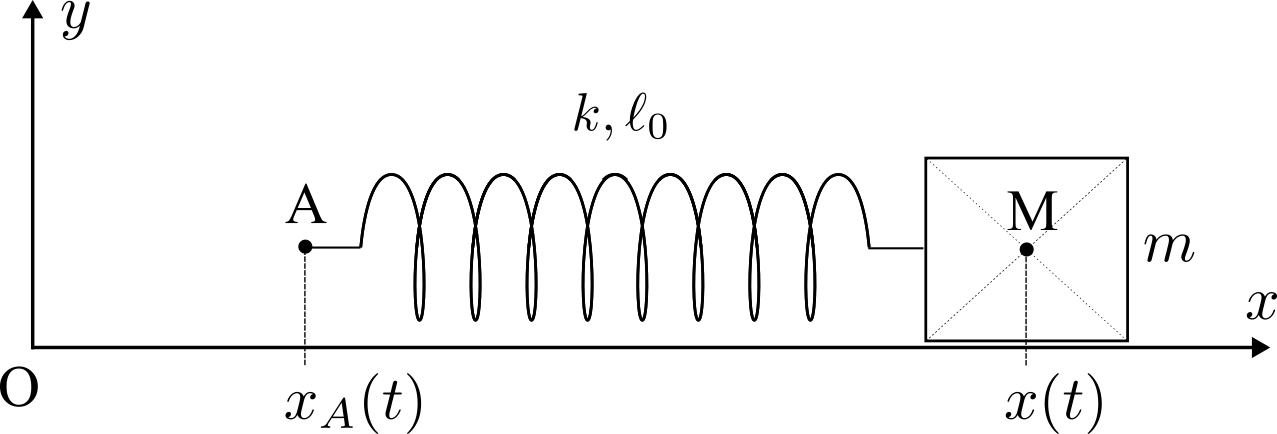
(d'après CCINP)On considère un solide de masse m, assimilable à un point M, lié à un ressort à spires non jointives de raideur k, de longueur à vide \(\ell_0\)
astreint à se déplacer sur l'axe (O, x) horizontal.
L'extrémité gauche du ressort est le point noté A.
A \(t = 0\), le ressort n'est ni étiré ni comprimé, le point M est immobile et A est en O : \(x(t=0) = \ell_0\) et \(x_A(t=0) = 0\) .
Le point A est poussé vers le point M à vitesse constante : \(\vec v_A = V_0 \, \ex\) avec \(V_0 > 0\).
On note f le coefficient de frottement solide entre M et le plan (xOy).
- Montrer que pour tout \(t \lt t_1\), le solide reste immobile. Exprimer \(t_1\) en fonction de f, g, \(V_0\) et \(\omega_0^2=k/m\).
- On note \(t^\prime = t - t_1\). Déterminer l'expression de \(x(t^\prime)\) pour \(t^\prime > 0\) et commenter.
- Le solide cesse-t-il de glisser pour \(t^\prime > 0\) ? On pourra par exemple représenter la force exercée par le ressort \(F_x(t^\prime)\) ansi que la vitesse de M, \(\dot x (t^\prime)\) et analyser ces courbes.
- Déterminer la puissance des forces de frottements, commenter.
Prérequis :
- Lois de Coulomb du frottement solide.
- L'expression "ressort à spires non jointives" signifie que le ressort peut travailler en élongation et en compression (comme un amortisseur de voiture).
Savoir-faire :
- Ecrire une condition de non glissement.
- Résolution d'une équation différentielle du type "oscillateur harmonique" avec second membre ni constant ni harmonique.
- Expression de \(t_1\)
- Mouvement pour \(t \gt t_1\)
- Les frottements solides peuvent-ils à nouveau stopper les oscillations (plus durablement qu'au changement de sens des oscillations) ?
- Puissance des frottements