Spire en rotation
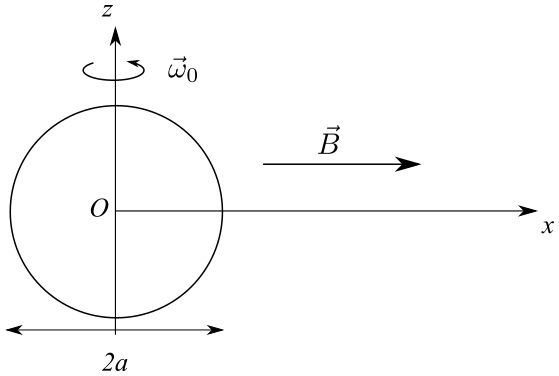
(d'après CCINP)Soit une spire conductrice, circulaire, de rayon a, de masse m animée d’un mouvement de rotation autour d’un axe fixe vertical, passant par son centre.
Cette spire est soumise à un champ magnétique extérieur \(\vec B = B \ex\) constant.
On négligera le champ magnétique créé par le courant induit devant le champ magnétique extérieur ainsi que tout frottement.
On note : \(\vec n\) le vecteur normal à la spire, \(\theta\) l’angle \((\ex, \vec n)\), \(R = 1 \Omega\) la résistance de la spire, \(S = 0,4 \si[2]m\) la surface de la spire,
\(J_\Delta\) le moment d’inertie de la spire par rapport à son axe de rotation, \(\omega_0 = 10 \si{rad/s}\) la vitesse angulaire de rotation initiale de la spire.
- Justifier qualitativement le mouvement ultérieur de la spire en l’absence de forces motrices extérieures.
- Déterminer la force électromotrice induite par le mouvement de la spire.
- Déterminer l’équation différentielle vérifiée par \(\theta\).
- Déterminer le moment \(\Gamma_\Delta\) par rapport à l’axe de rotation qu’il faut exercer pour entretenir la rotation à vitesse angulaire constante \(\omega_0\) lorsque la spire est placée dans un champ magnétique de 1 T.
Prérequis :
- Phénomène d'induction, loi de Faraday, loi de modération de Lenz.
- Moment magnétique d'un circuit (cf. dipôle magnétique), actions subies par un dipôle placé dans un champ.
- Théorème du moment cinétique.
- Mouvement ultérieur
- fem
- Equation différentielle
- Moment