Régime transitoire

Prérequis :

• Propriétés de continuité de certaines grandeurs électriques.
• Modèles limites de L et C lorsque \(t = 0^+\) et \(t \rightarrow \infty\).
• Caractérisation du régime pseudo-périodique.

Savoir-faire :

• Schéma circuit équivalent-simplifié aux instants \(t = 0^+\) et \(t \rightarrow \infty\) (un schéma dans chaque cas), pour en déduire les grandeurs électriques sans calcul.
• Mise en œuvre des lois de Kirchhoff.

1. \(t = 0^+\)
Solution

Rappels :
- la tension aux bornes d'un condensateur est continue ;
- l'intensité dans une bobine est continue.
- Lorsque \(t \rightarrow \infty\), le régime permanent est atteint : toutes les grandeurs électriques sont constantes.

Compte tenu des conditions initiales :


• \(u_C(0^+)=u_C(0^-)=\displaystyle\frac{q_0}{C}=0\) : à cet instant, le condensateur se comporte comme un fil.
• \(i_L(0^+)=i_L(0^-)=0\) : à cet instant, la bobine se comporte comme un interrupteur ouvert.

Rq - La fermeture du circuit provoque une variation très rapide des courants et des tensions, ce qui correspond à un régime haute fréquence pendant un temps très court : on retrouve ainsi les modèles limites de L et C.
Il est essentiel de faire un schéma en remplaçant L et C par leurs modèles limites.
On trouve \(i(0^+)=i_C(0^+)=\displaystyle\frac{E}{R}\), \(i_R(0^+)=0\) et \(u(0^+)=0\).




2. \(t \rightarrow \infty\)
Solution

\(u_C=cte \Rightarrow i_C=C\displaystyle\frac{du_C}{dt}=0\) : le condensateur se comporte comme un interrupteur ouvert.
\(i_L=cte \Rightarrow u_L=L\displaystyle\frac{di_L}{dt}=0\) : la bobine se comporte comme un fil.
Il est essentiel de refaire un schéma en remplaçant L et C par leurs modèles limites.
On trouve \(i(+\infty)=i_L(+\infty)=\displaystyle\frac{E}{R}\), \(i_R(+\infty)=0\) et \(u(+\infty)=0\).




3. \(i(t)\)
Solution

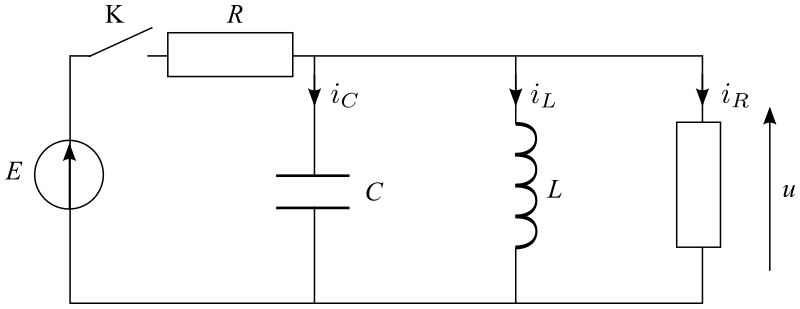
On cherche une équation différentielle en i, on cherche donc à exprimer toutes les grandeurs électriques en fonction de i.
On a 4 courants inconnus, il faut donc écrire 4 équations.
Loi des noeuds : \(i=i_C+i_L+i_R\)    (1).
Egalité des tensions pour C, L et R en dérivation (2 mailles) : \(u_C=u\)    (2) et \(u_L=u\)    (3)
Maille avec le générateur et u (sans expliciter u) : \(E=R i + u\)    (4)
(4) permet d'exprimer u en fonction de i     (5).
(2) et (5) donnent \(i_C\) en fonction de i.
(3) et (5) fournissent \(\displaystyle\frac{di_L}{dt}\) en fonction i.
Il suffit alors de dériver (1) par rapport au temps et d'injecter les résultats précédents.
On obtient : \(\displaystyle\frac{d^2i}{dt^2}+\frac{2}{RC}\frac{di}{dt}+\frac{1}{LC}i=\frac{1}{LC}\frac{E}{R}\).
Ou encore : \(\displaystyle\frac{d^2i}{dt^2}+\frac{\omega_0}{Q}\frac{di}{dt}+\omega_0^2i=\omega_0^2 i_\infty\).





4. Régime pseudo-périodique
Solution

Le régime pseudo-périodique correspond à des oscillations amorties. Le discriminant de l'équation caractéristique associée à l'équation différentielle homogène doit donc être négatif : \(\Delta \lt 0\).
On trouve \(R>\sqrt{\displaystyle\frac{L}{C}}\). Ce résultat est logique : lorsque R est grande, le courant est plus important dans les branches contenant L et C qui constituent un système oscillant.