A partir d'un oscillogramme
On considère un filtre dont la fonction de transfert est la suivante : \(\underline H(j\omega) = \dfrac{H_0}{1-\wwoc+j\dfrac{1}{Q}\wwo}\)
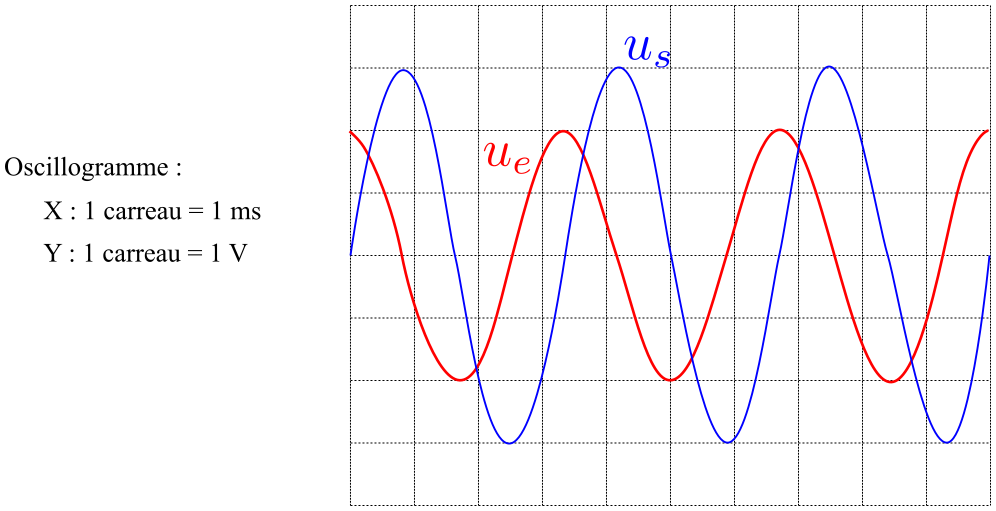
- Quelle est la nature du filtre ?
Tracer l'allure du diagramme de Bode en gain puis en phase. - Déterminer \(H_0\), \(\omega_0\) et Q en utilisant l’oscillogramme donné.
En régime continu, le filtre donne une tension de sortie égale à la tension d’entrée.
Savoir-faire :
- Analyse asymptotique (i.e. en basse fréquence et en haute fréquence) d'une fonction de transfert afin de déterminer la nature d'un filtre.
- Tracé des asymptotes du diagramme de Bode à partir de l'analyse asymptotique de la fonction de transfert.
- Nature du filtre
- Caractéristiques du filtre