Et la lumière fut
(d'après CCINP, Mines-Télécom)Une ligne haute tension assimilable à un fil droit infini selon l’axe (Oz) transporte un courant sinusoïdal \(i(t)\) de fréquence \(f = 50 \si{Hz}\) et de valeur efficace
\(I = 1000 \si A\).
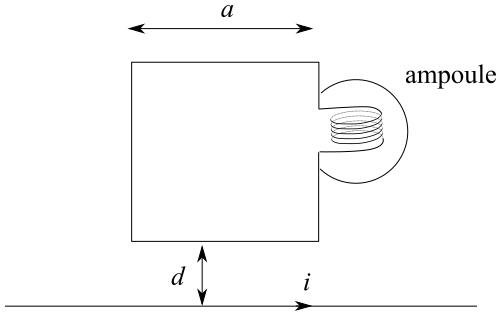
On approche de cette ligne haute tension une bobine plate de N spires carrées de côté \(a = 30 \si{cm}\) à une distance \(d = 2 \si{cm}\).
Cette bobine d’inductance propre et de résistance négligeables est fermée sur une ampoule qui s’éclaire si la tension efficace E à ses bornes est supérieure à 1,5 V.
On utilisera les coordonnées cylindriques \(\repcyl{O}\).
On se trouve ici dans l’approximation des régimes quasi-stationnaires (ARQS).
- Donner la définition et la condition de validité de l’ARQS. Justifier ici le choix de l’ARQS.
Dans ce cadre, on peut négliger le courant de déplacement dans les équations de Maxwell. - Déterminer en coordonnées cylindriques le champ magnétique \(\vec B (r)\) créé dans tout l’espace par cette ligne haute tension.
- Déterminer le flux magnétique total créé par cette ligne haute tension à travers la bobine plate.
- En déduire le nombre de spires N nécessaires pour que l’ampoule puisse s’éclairer.
Faire l’application numérique.
Prérequis :
- Définition de l'ARQS.
- Théorème d'Ampère.
- Loi de Faraday (induction).
Savoir-faire :
- Calcul du flux d'un champ non uniforme à travers une surface.
- ARQS
- \(\vec B (r)\)
- Flux magnétique
- Nombre de spires