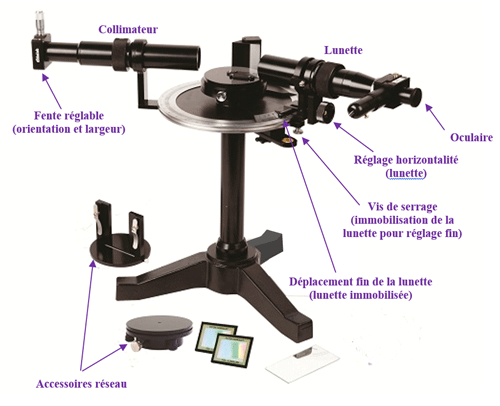
Vidéo Description / Vocabulaire : collimateur, lunette autocollimatrice, réticules...
Vidéo Utilisation : lame semi-réfléchissante sur la lunette, réglage de la fente source du collimateur
Vidéo Réglage du goniomètre : réglage de la lunette à l'infini par autocollimation, réglage du collimateur à l'infini
Cliquer sur le bouton "à la minute" le plus à droite (flèche rouge)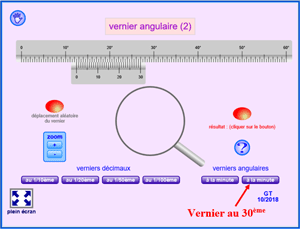
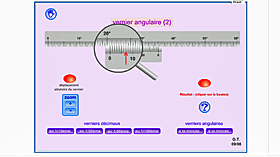Vidéo Mesure du minimum de déviation \(D_m(\lambda_0)\) avec un prisme
L’étude du prisme permet d’établir que l’indice du prisme est donné par la relation : \(n(\lambda_0 ) = \displaystyle\frac{\sin \left( \frac{A + D_m(\lambda_0)}{2} \right)}{\sin \left( \frac{A}{2} \right)}\) où A est l’angle au sommet du prisme et \(D_m(\lambda_0)\), le minimum de déviation pour la radiation de longueur d’onde \(\lambda_0\) dans le vide.
Vidéo Mesure du minimum de déviation \(D_m(\lambda_0)\) avec un réseau
Définition - La déviation dans l’ordre p pour la raie de longeur d'onde dans le vide \(\lambda_0\) est : \(D_{p,\lambda_0} = \left| \theta_p - \theta_i \right|\)
Théorème - La déviation \(D_{p,\lambda_0}\) passe par un minimum noté simplement \(D_m\) lorsque : \(\theta _p = -\theta _i\)
Le plan du réseau est alors le plan bissecteur des rayons incidents et diffractés dans l’ordre p (cf. schéma).
On a alors : \(2\sin \displaystyle\frac{D_m}{2} = p\frac{\lambda _0}{a}\)
Application à la spectroscopie : la mesure de \(D_m\) permet de déterminer \(\lambda_0\) connaissant p et a.
Il faut donc préalablement étalonner le réseau à l'aide d'une radiation de longueur d'onde dans le vide connue pour déterminer a.
Vidéo Mesure de l'angle au sommet du prisme.
Vernier