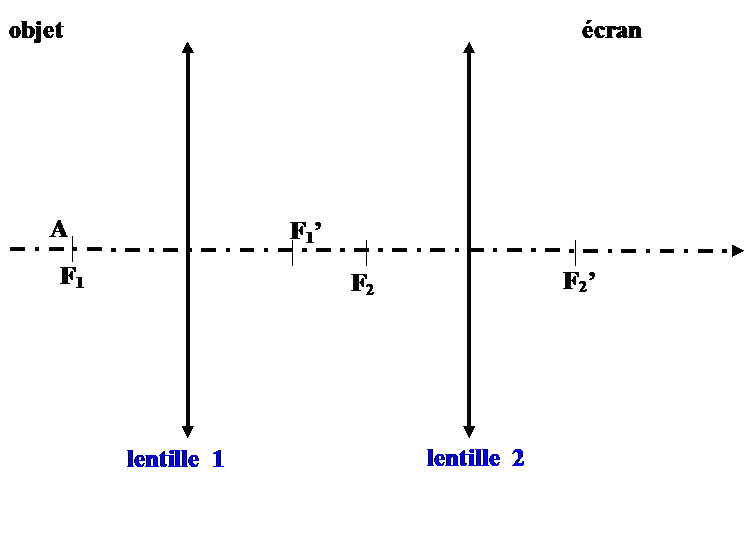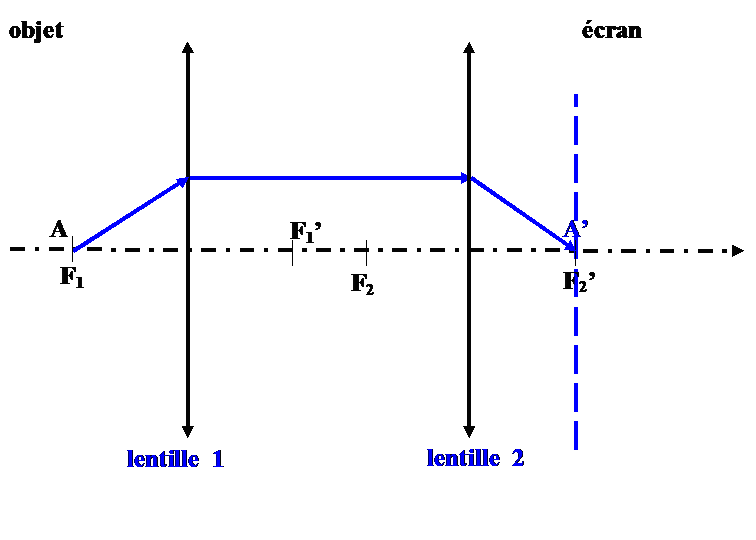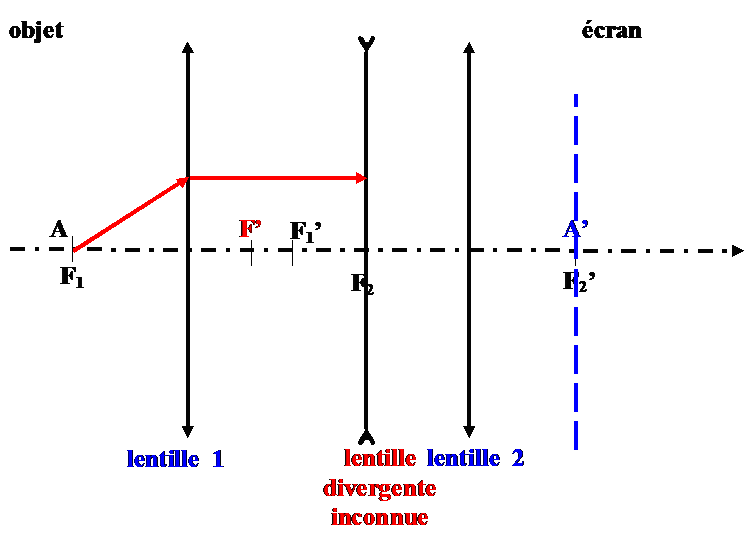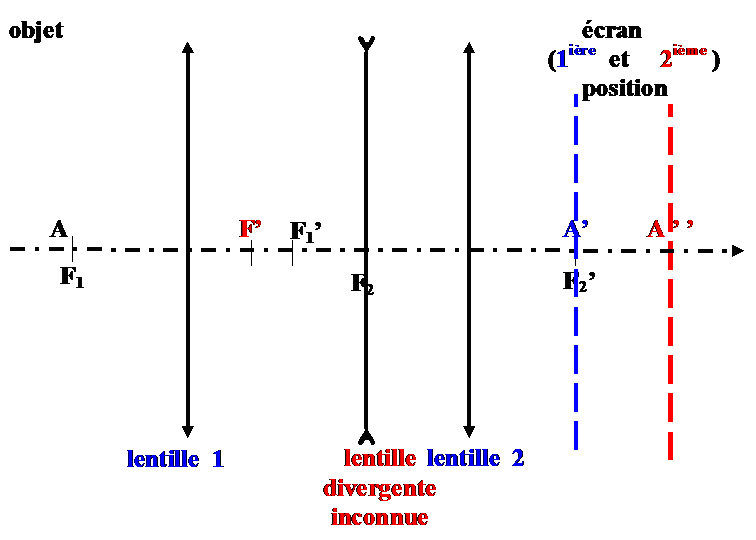
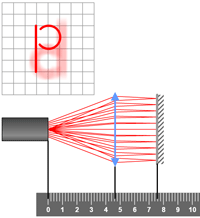
Une source éclaire un objet en forme de lettre "P" (figures ci-dessous). Un faisceau issu d'un point objet réel A de cette lettre est représenté. Ce faisceau objet rencontre une lentille mince convergente de centre O et de distance focale image \(f'\). Un miroir plan est positionné derrière la lentille. L'aspect de l'écran, placé dans le plan de l'objet (ce peut être le cache dans lequel la lettre "P" est percée), est visible au-dessus de la source.
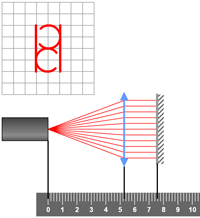
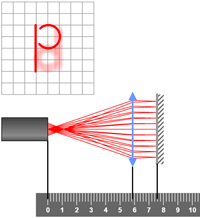
Sur les trois figures, seule la lentille a été déplacée de gauche à droite.

Utiliser l'applet :
- cliquer sur le bouton "faisceau" ;
- déplacer la lentille et observer l'aspect de l'écran (obtenir les situations des figures précédentes) ;
- en déduire un protocole de mesure de la distance focale d'une lentille mince convergente (cliquer sur "principe" et "protocole" pour confirmation).

Utiliser l'applet pour déterminer si la position du miroir influe sur la mesure.
Justifier ce résultat à l'aide d'un diagramme de la forme : \( \textrm{objet} \mathop {\longleftrightarrow} \limits^{S.O} \,\, ? \,\, \mathop {\longleftrightarrow} \limits^{S.O} \,\, ? \,\, ...\)
(S.O. = système optique = lentille, miroir, dioptre...).

Commenter la simulation ci-dessous (logiciel Optgéo) : justifier que l'orientation du miroir est sans effet (tant que le faisceau réfléchi passe par la lentille).

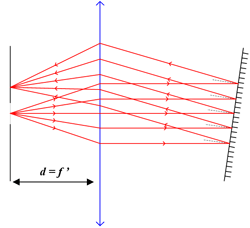
Justification de la méthode d'autocollimation
Dans le cas \( \overline{\textrm{A}\textrm{O}} = f' \), faire une construction représentant la marche de deux rayons issus du point objet et justifier que l'image A' de A par la lentille se forme bien dans le même plan que l'objet.

En pratique, d'après ce qui précède, il est possible d'accoler le miroir plan à la lentille.

D'après ce qui précède, peut-on accoler lentille et miroir ? Tester.
Effectuer la mesure de la distance focale d'une lentille mince convergente et estimer l'incertitude de mesure.
Cette méthode est-elle applicable à une lentille divergente ?

Les aspects pratiques (savoir-faire) et théoriques de la méthode d'autocollimation doivent être connus.

Décrire le protocole expérimental et préciser ce qu'on mesure.

On considère la seule lentille \(L_2\). Déduire du diagramme précédent quels sont les points objet et image (sur l'axe optique) conjugués par \(L_2\).
En utilisant la relation de conjugaison de Newton pour la lentille \(L_2\), en déduire que la focale cherchée est donnée par : \( f'= -\displaystyle\frac{f'^2_2}{\overline{\textrm{A}'\textrm{A}^{\prime\prime}}} \)

Rappel - Relation de conjugaison de Newton (A et A' sont conjugués par une lentille de focale \(f'\) de foyers F et F') : $$ \overline{\textrm{F}\textrm{A}} \cdot \overline{\textrm{F}'\textrm{A}'} = -f'^2 $$

applet (manipuler l'applet pour retrouver le principe des méthodes de Bessel et Silberman).

Méthode de Bessel - Etude théorique
Démontrer que la distance, notée D, entre l'objet et l'écran pour former une image de cet objet par une lentille mince L de focale \(f'\) est : $$ D \geq 4 f' $$ Dans le cas \(D \gt 4 f' \), on observe une image sur l'écran pour deux positions différentes de la lentille L. On note d la distance entre ces deux positions.
Etablir la relation entre \(f'\), D et d.
Montrer que les grandissements de ces images sont inverses l'un de l'autre.

Peut-on utiliser une lentille divergente ?
Déterminer la focale d'une lentille par la méthode de Bessel et effectuer un calcul d'incertitudes.