Extrait e3a PC 2008
1 / CONDUCTANCE THERMIQUE A TRAVERS UN TUBE CYLINDRIQUE
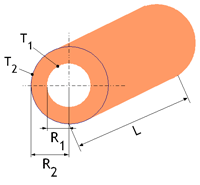
Considérons un tube cylindrique d’axe Oz, de rayon intérieur R1 de rayon extérieur R2 et de très grande longueur (figure 1).
Le tube est réalisé dans un matériau de conductivité thermique notée λ.
1*a. Dans le cas général, rappeler la loi de Fourier qui relie le vecteur densité de courant thermique, noté \( \vec j _Q\) , au gradient de la température.
1*b. Justifier en quelques mots que la conductivité thermique, telle qu’elle apparaît dans la loi de Fourier, est toujours un nombre positif.
Le système est en régime permanent : la température T(r) en un point M du tube ne dépend donc que de r, la distance de M à l’axe (coordonnées cylindriques).
Les températures de surface sont notées T1 = T(R1) et T2 = T(R2).
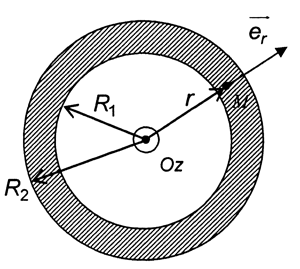
1*c. Préciser la direction du vecteur \( \vec j _Q\) dans le tube.
1*d. Exprimer la puissance thermique \(\mathcal{P}_{Th}\) sortant d’un cylindre de rayon r (R1 < r < R1) et de longueur ℓ, en fonction de jQ(r) et r.
1*e. En appliquant le premier principe de la thermodynamique à un système correctement choisi, montrer que la puissance thermique \(\mathcal{P}_{Th}\) est indépendante de r.
1*f. En déduire l’expression de la température T(r) en fonction de \(\mathcal{P}_{Th}\), r, R1, λ, T1 et ℓ.
1*g. Établir que la puissance thermique \(\mathcal{P}_{Th}\) peut s’écrire : \(\mathcal{P}_{Th}\) = g ℓ(T1 – T2), (1)
en exprimant g en fonction de λ, R1 et R2.
1*h. Calculer g pour un tube possédant les caractéristiques suivantes : conductivité thermique λ = 0,40 kWm-1K-1, rayons R1 = 8,0 mm et R2 = 8,5 mm.